5.6. Matice = CTRL + SHIFT + ENTER
Průvodce studiem
PRŮVODCE STUDIEM
Tato podkapitola je přidaná "na poslední chvíli", proto se poněkud vymyká zařazení do struktury učiva. Obsah podkapitoly je procvičován v rámci 10. úkolu.
Nepodceňujte, prosím, tuto podkapitolu, protože její náplň je pro vaše další studium velmi užitečná a důležitá.
Cíle kapitoly
CÍL PODKAPITOLY
Naučit se pracovat s matematickou maticí v aplikaci EXCEL, umět sčítat, násobit, transponovat a invertovat matice, umět vypočítat determinant čtvercové matice.
Klíčová slova
KLÍČOVÁ SLOVA
Matice, transponovaná matice, inverzní matice, determinant, trojhmat.
Čas ke studiu
ČAS POTŘEBNÝ KE STUDIU
Pokud máte jisté povědomí o pojmu "matematická matice" a nemusíte si složitě opakovat matematiku, technika práce v aplikaci by nemusela zabrat více, než půl hodiny.
K zapamatování
Trocha teorie, doufám, nezabije!
Matice typu (m x n)
Tímto pojmem budeme nazývat obdélníkové pole m x n reálných čísel, (tzv. prvků matice), uspořádaných do m řádků a n sloupců. Matice budeme označovat velkými písmeny, prvky matice odpovídajícími malými písmeny se dvěma indexy, přičemž první index udává číslo řádku, druhý číslo sloupce, ve kterém se prvek nachází.
Prvky matice se stejnými indexy tvoří hlavní diagonálu matice.
(Velice zjednodušeně řečeno: hlavní diagonála vede z levého horního rohu matice do pravého dolního rohu matice.)
Má-li v matice všechny prvky pod (respektive nad) hlavní diagonálou rovny nule, nazýváme matici horní (respektive dolní) trojúhelníkovou maticí.
Matici, která má stejný počet řádků, jako sloupců, nazýváme čtvercovou maticí.
Matici, jejíž všechny prvky jsou rovny nule nazýváme nulovou maticí.
Čtvercovou matici, která má všechny prvky mimo hlavní diagonálu rovny nule nazýváme diagonální maticí.
Diagonální matici, která má na hlavní diagonále všechny prvky rovny jedné nazýváme jednotkovou maticí a označujeme ji E.
Transponovaná matice k matici A typu (m x n) rozumíme matici A s horním indexm T typu (n x m).
(Lidově řečeno: zaměníme řádky a sloupce. K rozvrhu hodin, kde jsou názvy dnů v levém sloupci a hodiny v jednotlivých dnech se nachází na řádcích, je transponovanou maticí rozvrh, kde jsou názvy dnů nahoře a rozvrh jednoho dne se nachází ve sloupci.)
Rovnost matic. Matice A a B jsou si rovny, jsou-li stejného typu a mají-li na odpovídajících si místech stejné prvky. Zapisujeme A = B.
Symetrická matice. Reálnou čtvercovou matici A nazveme symetrickou, jestliže pro ni platí A = A s horním indexem T.
Součtem matic A a B stejného typu (m x n) nazýváme matici A + B typu (m x n).
Rozdílem matic A a B stejného typu (m x n) nazýváme matici A + (-1) · B typu (m x n). Označujeme ji A - B.
Součinem matic A typu (m x n) a B typu (n x p) nazýváme matici C typu (m x p), pro jejíž prvky platí:
![]()
(Opět hlas lidu: Při násobení matic se musí shodovat počet sloupců první matice s počtem řádků druhé matice. Výsledný součin je matice, která má počet řádků jako první matice a počet sloupců jako druhá matice. Na pořadí matic v součinu ZÁLEŽÍ!)
Hodností matice A nazýváme maximální počet lineárně nezávislých řádků nebo sloupců matice A. Označujeme ji h(A).
Hodnost matice typu (m x n) lze určit pomocí tzv. Gaussova algoritmu. Ekvivalentními úpravami (viz níže) převedeme matici např. na horní trojúhelníkovou, vyškrtneme z ní všechny lineárně závislé a nulové řádky. Hodnost takto upravené matice je rovna počtu nenulových řádků.
Determinantem čtvercové matice A řádu n nazýváme číslo
![]() ,
,
kde sčítáme přes všechny permutace P množiny {1, 2, ..., n}. Veličina Z(P) je tzv. znaménko permutace P.
Ekvivalentními úpravami rozumíme:
a) vzájemnou výměnu libovolných řádků,
b) vynásobení libovolného řádku nenulovým číslem,
c) přičtení lineární kombinace ostatních řádků (speciálně přičtení násobku jiného řádku) k některému řádku,
d) vynechání řádku, který je lineární kombinací ostatních řádků (speciálně vynechání nulového řádku).
Všechny čtyři výše uvedené úpravy lze provádět i se sloupci matice.
5.6.1. A jak vypadá teorie v EXCELu?
Matice se v aplikaci EXCEL nazývá "pole". Skládá se tedy z více buněk. Má-li matice 3 řádky a 2 sloupce, v EXCELU budeme k jejímu zápisu potřebovat 6 buněk a do každé zapíšeme konkrétní hodnotu.
Chceme-li ručně vypsat matici do řádku vzorců a nevypisovat hodnoty do jednotlivých buněk, použijeme tzv. maticovou konstantu.
Maticové konstanty jsou uzavřeny ve složených závorkách ( { } ), hodnoty v jednotlivých sloupcích se oddělují středníkem (;), hodnoty v různých řádcích se oddělují znakem svislé čáry ( | ).
Řešení, návody
NAPŘÍKLAD
Chceme-li zobrazit hodnoty 10, 20, 30 a 40, zadáme je následujícím způsobem:
{10;20;30;40}.
Tato maticová konstanta se označuje jako matice 1-krát-4 a představuje odkaz 1-řádek-krát-4-sloupce.
Pokud chceme například zobrazit hodnoty 10, 20, 30 a 40 v jednom řádku a hodnoty 50, 60, 70 a 80 v řádku hned pod ním, zadáme maticovou konstantu 2-krát-4:
{10;20;30;40|50;60;70;80}.
Maticový vzorec může provést několik výpočtů a potom vrátit jeden nebo několik výsledků. Maticové vzorce počítají na základě dvou nebo více množin hodnot, neboli maticových argumentů. Každý maticový argument musí obsahovat stejný počet řádků a sloupců. Maticové vzorce vytvoříme stejně jako jiné vzorce.
Jediný rozdíl spočívá v tom, že se vzorec zadává stisknutím kláves
CTRL+SHIFT+ENTER.
Některé předdefinované funkce představují maticové vzorce. Pokud chceme získat správný výsledek, je třeba tyto vzorce zadat jako matice.
5.6.2. SOUČET MATIC
Sčítat se dají pouze matice, které se shodují v počtu řádků a sloupců. pokud mají matice rozdílný tvar, sčítat je nelze!
Součet matic stejného tvaru si ukážeme na příkladě:
Příklad
PŘÍKLAD
Sečtěte matice A + B.
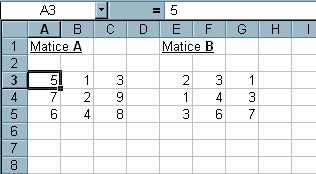
Obr. 5-61
Řešení:
Kurzor postavíme na pozici buňky, kam chceme uložit výsledek. V ideálním případě označíme pole 3x3 buňky, abychom dostali rovnou výslednou matici. Můžeme označit i pole větší (přebytečné buňky vykážou po výpočtu chybu a můžeme je smazat).
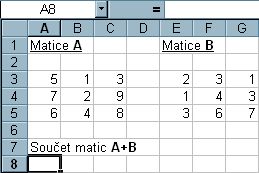
Obr. 5-62
Levým tlačítkem myši klikneme na znak " = "před řádkem vzorců.
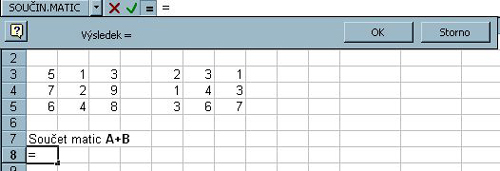
Obr. 5-63
Označíme oblast matice A, na numerické klávesnici zmáčkneme + a označíme oblast matice B.
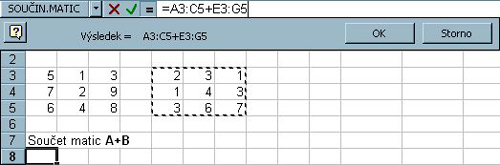
Obr. 5-64
Místo OK nebo ENTER použijeme TROJHMAT: CTRL + SHIFT + ENTER !!!!!!!!!
Pokud byla označena pouze jedna buňka (a v okně jste použili OK), ještě nemáme správný výsledek a je nutný následující postup:
1. Označíme pole (v našem případě 3x3 buňky), přičemž buňku s výsledkem necháme v levém horní rohu.
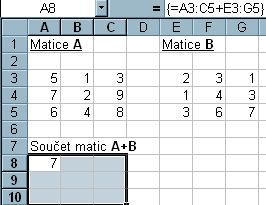
Obr. 5-65
2. Zmáčkneme klávesu F2.
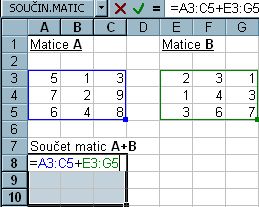
Obr. 5-66
3. Použijeme TROJHMAT (CTRL + SHIFT + ENTER)
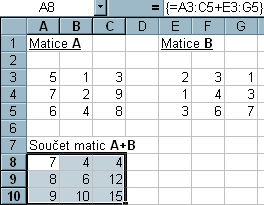
Obr. 5-67
5.6.3. SOUČIN MATIC
Vrátí maticový součin dvou polí. Výsledkem je matice se stejným počtem řádků jako v prvním poli a s počtem sloupců jako v druhém poli.
Příkaz EXCELu: SOUČIN.MATIC(pole1;pole2)
Pole1, pole2 jsou matice, které chceme vynásobit.
Komentář
- Počet řádků v prvním poli musí být stejný jako počet sloupců v druhém poli, a obě pole musí obsahovat pouze čísla.
- Pole pole1 a pole2 mohou být zadána jako oblast buněk, maticová konstanta nebo odkazy.
- Pokud jsou některé buňky prázdné nebo obsahují text, nebo počet sloupců v prvním poli je jiný než počet řádek ve druhém poli, vrátí funkce SOUČIN.MATIC chybovou hodnotu #HODNOTA!.
- Vzorce, jejichž výsledkem je matice, musí být zadány jako maticové vzorce.
Příklad
PŘÍKLAD
Násobte matice A a B, v abecedním pořadí. (A.B).

Obr. 5-84
Řešení:
Matice A má 3 řádky, matice B má 3 sloupce, součin těchto buněk je tedy možný. Výsledná matice bude mít 3 řádky a 3 sloupce.
Kurzor postavíme na pozici buňky, kam chceme uložit výsledek. V ideálním případě označíme pole 3x3 buňky, abychom dostali rovnou výslednou matici. Můžeme označit i pole větší (přebytečné buňky vykážou po výpočtu chybu a můžeme je smazat).
Z menu vybereme položku VLOŽIT a z rolety příkaz Funkce... (lze nahradit klepnutím na znak = před řádkem vzorců).
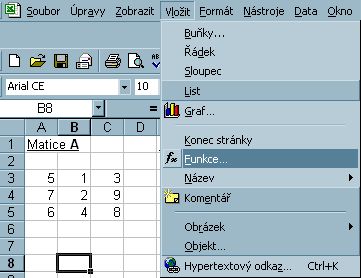
Obr. 5-85
Z funkcí vybereme skupinu Matematické a vyhledáme pojem SOUČIN.MATIC.
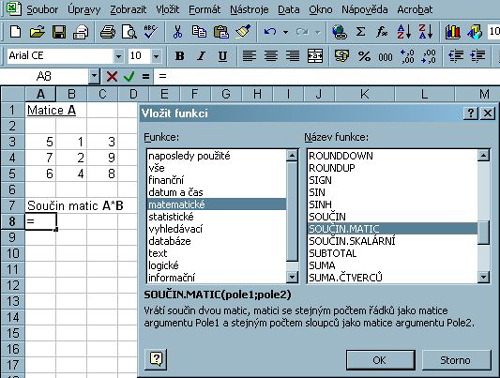
Obr. 5-86
Poté se objeví okno, ve kterém definujeme pole (matice) prostřednictvím ikony ![]()
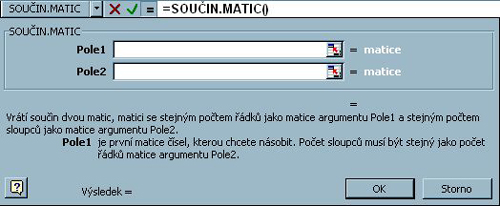
Obr. 5-87
Pro Pole1 označíme matici A, pro Pole2 označíme matici B.
Důležité!
DŮLEŽITÉ!!!
Pro výsledek je nutno použít TROJHMAT CTRL + SHIFT + ENTER.
Pokud bylo před výpočtem označeno pole, máte již výsledek.
Pokud byla označena pouze jedna buňka (a v okně jste použili OK), je nutný následující postup:
1. Označíme pole (v našem případě 3x3 buňky), přičemž buňku s výsledkem necháme v levém horní rohu.

Obr. 5-88
2. Zmáčkneme klávesu F2.
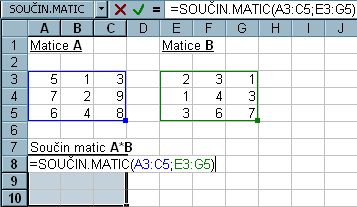
Obr. 5-89
3. Použijeme TROJHMAT (CTRL + SHIFT + ENTER).
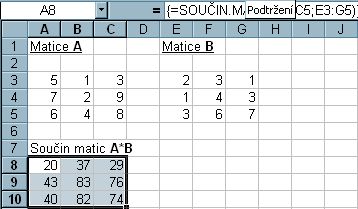
Obr. 5-90
5.6.4. INVERZNÍ MATICE
Vrátí matici inverzní k matici obsažené v zadaném poli.
Příkaz EXCELu: INVERZE(pole)
Matice, jejíž inverzní podobu chceme získat, musí být čtvercová, tedy musí mít stejný počet řádků a sloupců.
Poznámka:
- Pole může být zadáno jako oblast buněk (například A1:C3), jako maticová konstanta (například {1;2;3|4;5;6|7;8;9}) nebo jako příslušný název.
- Pokud jsou buňky v poli prázdné nebo obsahují text, funkce INVERZE vrátí chybovou hodnotu #HODNOTA!.
- Funkce INVERZE vrátí chybovou hodnotu #HODNOTA! také v případě, že pole nemá stejný počet řádků a sloupců.
- Vzorce, jejichž výsledkem je matice, musí být zadány jako maticové vzorce.
- Inverzní matice jsou, podobně jako determinanty, nejčastěji používány při řešení soustav matematických rovnic. Součin matice a matice k ní inverzní je jednotková matice (čtvercová matice, která má na hlavní diagonále jedničky a všechny ostatní prvky rovny nule).
- Funkce INVERZE je počítána s přesností na přibližně 16 míst. Při výpočtech proto může docházet jen k velmi malým numerickým chybám.
- Některé čtvercové matice nelze invertovat. Funkce INVERZE v takovém případě vrátí chybovou hodnotu #NUM!. Determinant matice, kterou nelze invertovat, je roven 0.
Příklad
PŘÍKLAD
K matici A nalezněte inverzní matici A s horním indexem -1.
Obr. 5-91
Řešení:
Kurzor postavíme na pozici buňky, kam chceme uložit výsledek. V ideálním případě označíme pole 3 x 3 buňky, abychom dostali rovnou výslednou matici. Můžeme označit i pole větší (přebytečné buňky vykážou po výpočtu chybu a můžeme je smazat).
Z menu vybereme položku VLOŽIT a z rolety příkaz Funkce... (lze nahradit klepnutím na znak = před řádkem vzorců).
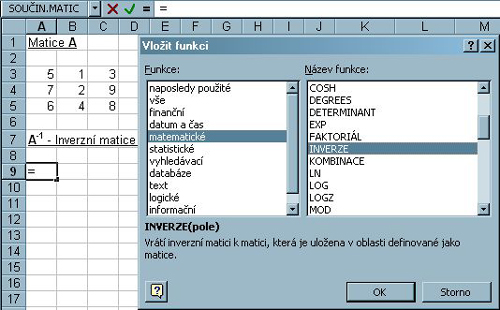
Obr. 5-92
Z funkcí vybereme skupinu Matematické a vyhledáme pojem INVERZE.
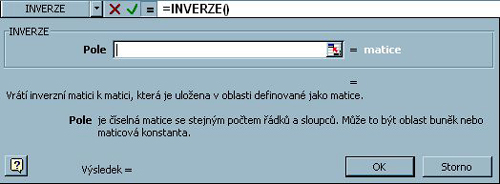
Obr. 5-94
Přes ikonu ukážeme na oblast matice A.

Obr. 5-94
Potvrdíme tlačítkem OK.
Výsledek je zatím pouze v jedné buňce.
Použijeme postup z předchozích textů (ano, přesně tak: Označit příslušně velkou oblast, použít F2 a trojhmat).
5.6.5. TRANSPONOVANÁ MATICE
Vrátí svislou oblast buněk ve tvaru vodorovné oblasti a naopak.
Funkce TRANSPOZICE se zadává jako maticový vzorec do oblasti se stejným počtem řádků a sloupců, jako je počet sloupců a řádků původní matice.
Slouží ke změně vertikální a horizontální orientace matice v listu.
Příkaz EXCELu: TRANSPOZICE(pole)
Příklad
PŘÍKLAD
Transponujte matici A a vytvořte matici A s horním indexem T.
Obr. 5-95
Řešení:
Nastavte kurzor na oblast, kterou bude zaujímat transponovaná matice (v našem případě je oblast velká 3 x 3 buňky).
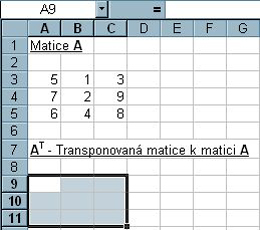
Obr. 5-96
Vyberte funkci TRANSPOZICE
(Menu: Vložit - Funkce... - vyhledávací - TRANSPOZICE)
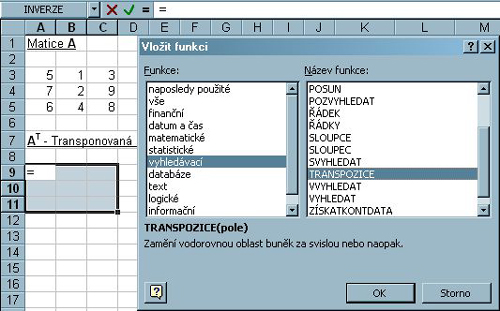
Obr. 5-97
V okně TRANSPOZICE pomocí ikony ukážeme na oblast matice A a vrátíme se do okna.
Místo OK nebo ENTER použijeme TROJHMAT (CTRL + SHIFT + ENTER).
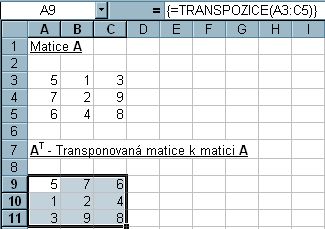
Obr. 5-98
Takto odpadá nutnost rozšíření (označení, F2, následný trojhmat).
5.6.6. DETERMINANT
Determinant je číslo.
Příkaz EXCELu: DETERMINANT(pole)
Pole musí být matice se stejným počtem řádků i sloupců (čtvercová).
Pole může být zadáno jako oblast buněk, například A1:C3, jako maticová konstanta, například {1;2;3|4;5;6|7;8;9}, nebo jako příslušný název.
Pokud je některá z buněk pole prázdná nebo obsahuje text, vrátí funkce DETERMINANT chybovou hodnotu #HODNOTA!.
Chybová hodnota #HODNOTA! je také vrácena, pokud není stejný počet řádků i sloupců.
Příklad
PŘÍKLAD
Vypočítejte determinant matice A.
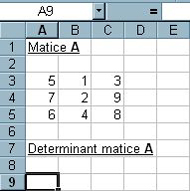
Obr. 5-99
Řešení:
Kurzorem označíme na buňku, ve které chceme výsledek.
Zvolíme funkci DETERMINANT
(Menu: Vložit - Funkce... - matematické - DETERMINANT)
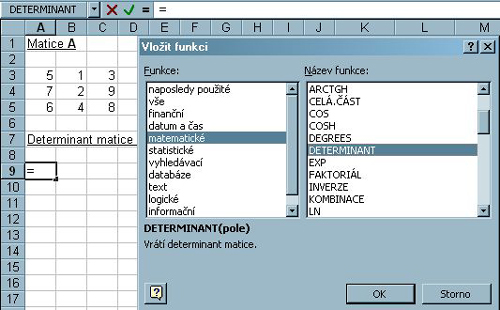
Obr. 5-100
V okně DETERMINANT označíme pomocí ikony a levého tlačítka myši oblast matice A a použijeme tlačítko OK nebo klávesu ENTER.
Výsledná hodnota je -54.
Operační program Rozvoj lidských zdrojů
Studijní opory s převažujícími prvky pro předměty teoretického základu studia
Číslo projektu: CZ.O4.01.3/3.2.15.1/0016